목차
1. 서론
2. 작동원리
3. 구현
1. 서론
다익스트라 알고리즘은 한 정점에서 다른 정점들까지의 최단 거리와 경로를 구하는 알고리즘이다. 단, 간선의 거리 정보는 항상 0 이상이어야 한다.
2. 작동원리
1. 방문하지 않은 정점 중 가장 시작점으로부터 거리가 짧은 정점으로 이동한다. 이 때, 해당 정점까지의 최단 거리는 확정된다.
2. 현재 정점과 인접한 모든 정점들 중 방문하지 않은 정점들을 돌면서 거리를 갱신시켜준다. 즉, 현재 정점까지의 최단 거리를 A, 현재 정점과 인접한 정점 V를 잇는 간선의 거리를 B, 현재까지 구한 V까지의 최단거리를 C라고 했을 때, A+B < C 이면 V까지의 최단 거리를 A+B로 갱신해준다는 의미이다.
위 과정을 아래에서 그림으로 한번 살펴보자. 아래 그림은 영문 위키 다익스트라 문서에서 가져왔다.
시작점부터의 i까지의 최단 거리를 담은 배열을 dis[i]라고 하고, i에서 j까지 간선의 정보를 d[i][j]라고 해보자.
빨간색의 정점은 현재 방문 중인 정점, 초록색 정점은 최단 거리가 확정된 정점이다.

시작점을 1로 잡고 dis[1]을 0으로 초기화해주었다.

dis가 제일 작은 것이 1번이므로 1번을 방문한다. 1번 정점까지의 최단 거리는 0으로 확정되었다. 1번과 인접한 정점들 2, 3, 6번을 돌며 거리를 갱신한다. 현재는 1번을 제외한 모든 정점까지의 거리가 무한대이므로 모두 갱신된다.
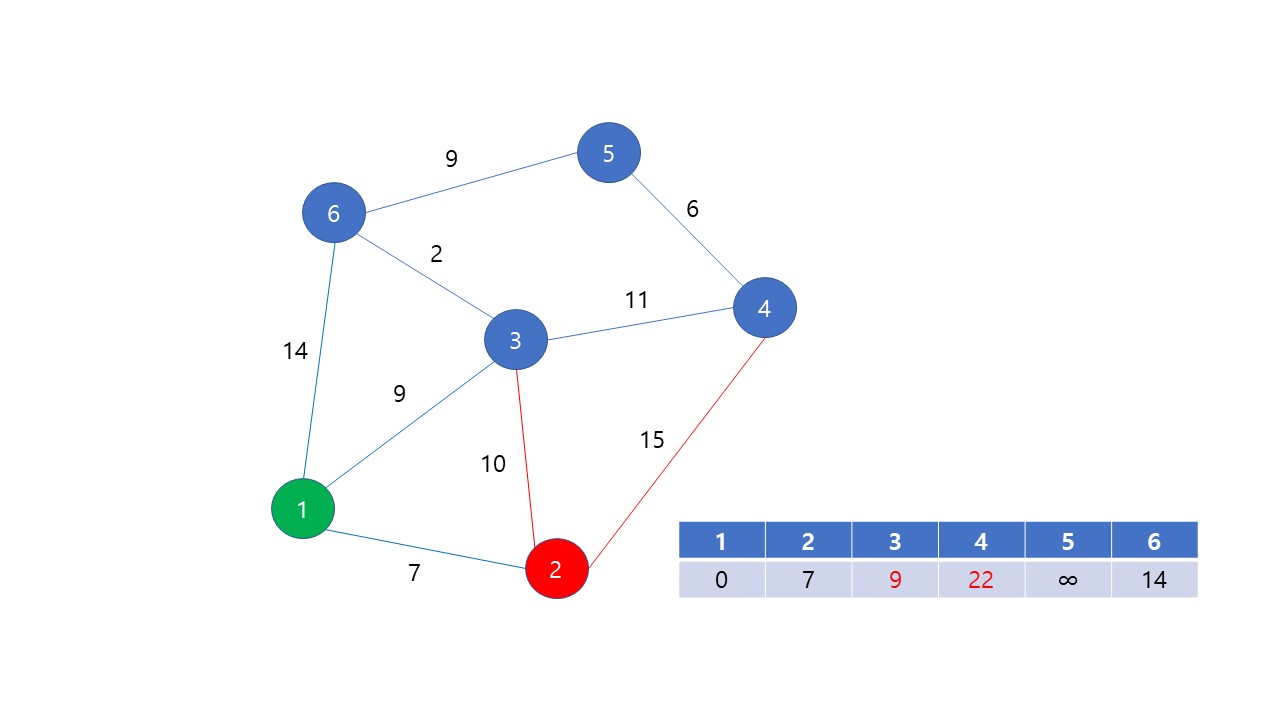
dis 배열에서 최단 거리가 확정되지 않은 것 중 가장 값이 작은 것이 2번이므로 2번을 방문한다. 2번 정점까지의 최단 거리가 7로 확정되었다. 2번과 인접한 정점은 1, 3, 4번인데 1번은 이미 방문했으므로 3, 4번을 돌며 거리를 갱신 시도한다. 하지만, 3번 정점까지의 최단거리는 갱신되지 않는다. dis[3] < dis[2] + d[2][3]이기 때문이다.
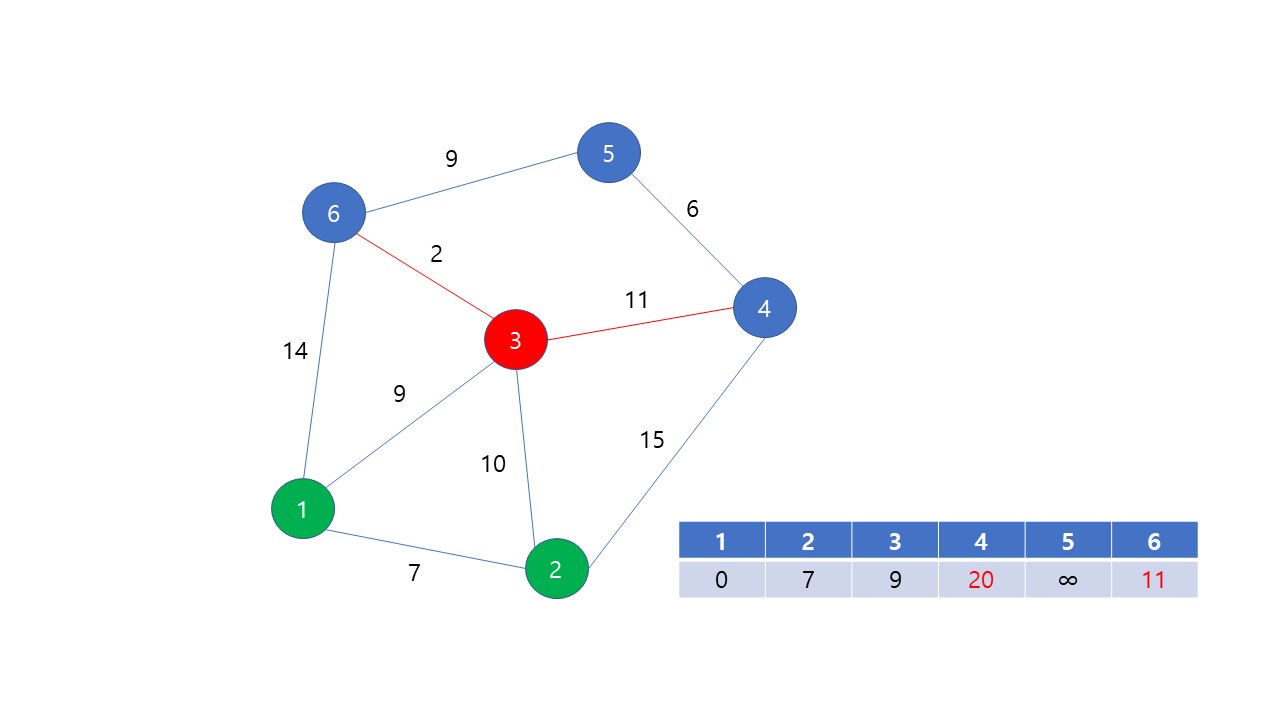
dis 배열에서 최단 거리가 확정되지 않은 것 중 가장 값이 작은 것이 3번이므로 3번을 방문한다. 3번 정점까지의 최단 거리가 9로 확정되었다. 3번과 인접한 정점은 1, 2, 4, 6번인데 1, 2번은 이미 방문했으므로 4, 6번을 돌며 거리를 갱신 시도한다.

dis 배열에서 최단 거리가 확정되지 않은 것 중 가장 값이 작은 것이 6번이므로 6번을 방문한다. 6번 정점까지의 최단 거리가 11로 확정되었다. 6번과 인접한 정점은 1, 3, 5번인데 1, 3번은 이미 방문했으므로 5번으로 가 거리를 갱신 시도한다.
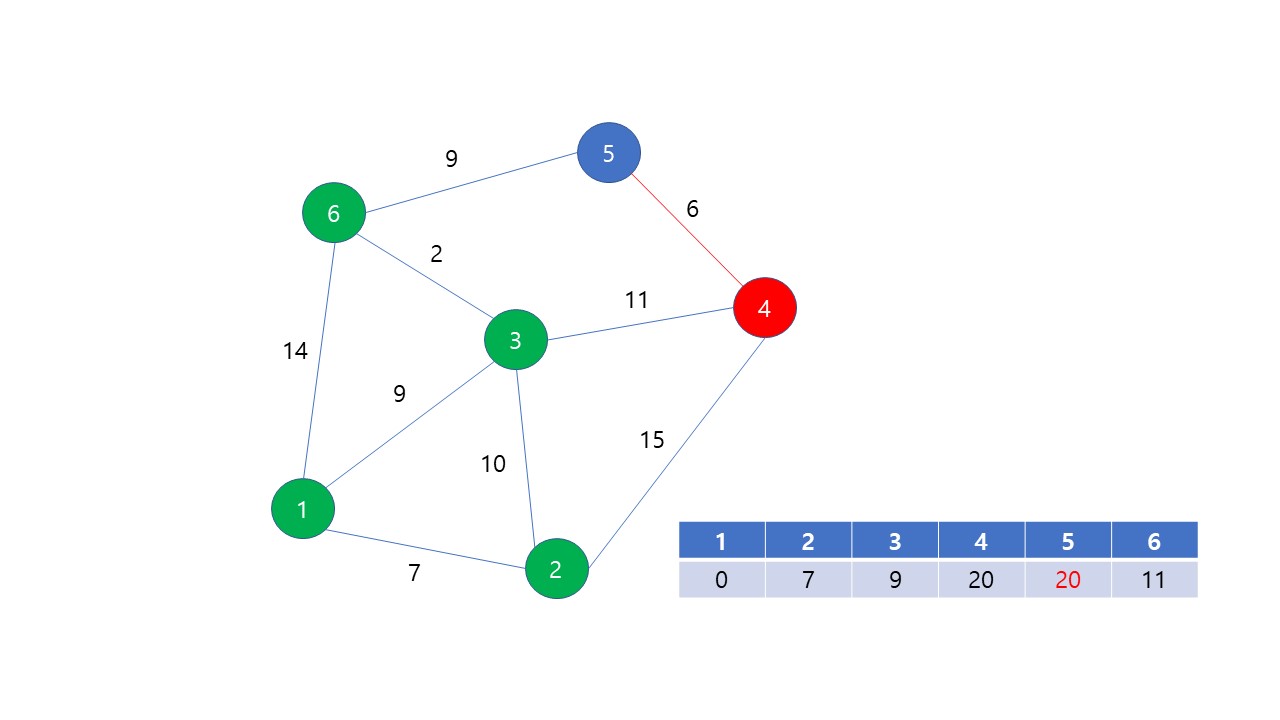
4번과 5번의 거리가 20으로 같다. 이럴 경우는 둘 중에 아무거나 방문해도 되는데 숫자가 작은 4번을 먼저 방문하는 것으로 해보자. 4번 정점까지의 최단 거리가 20으로 확정되었다. 4번과 인접한 정점은 2. 3. 5번인데 2, 3번은 이미 방문했으므로 5번으로 가 거리를 갱신 시도한다. 하지만, dis[5] < dis[4] + d[4][5]이므로 갱신되지 않는다.

마지막으로 5번 정점을 방문할 때는 아무것도 하지 않는다.
이 과정을 모두 끝내면 dis[i] 값이 시작점부터 i번까지의 최단 거리가 된다.
근데 위 과정들을 보면 궁금한 점이 하나 생기지 않는가? 매번 dis배열에서 최단 거리가 확정되지 않은 것 중에서 가장 값이 작은 정점을 방문한다. 이때, 왜 그 정점의 dis 배열 값은 이미 최단 거리인걸까? 나는 처음에 이 부분을 이해하기가 쉽지 않았다.
만약 아직 최단 거리가 확정되지 않은 정점 중에서 가장 dis 값이 작은 정점이 a라고 해보자. 근데 dis[a]가 실제 최단 거리보다 큰 값이라고 해보자. 이 말은 다른 임의의 정점 b를 통해서 a로 가는 최단 경로가 있다는 의미이다. 즉, dis[a] > dis[b] + d[b][a] 인 b 정점이 존재한다는 의미이다. 근데 a가 아직 최단 거리가 확정되지 않은 정점 중에서 가장 dis 값이 작은 정점이라고 했으니 b는 이미 방문한 정점일 것이다. 그런데, b를 방문했을 때, 이미 dis[a] = dis[b] + d[b][a]로 갱신이 되었어야한다. 그러므로, 아직 최단 거리가 확정되지 않은 정점 중에서 가장 dis 값이 작은 정점을 방문하면 그 정점까지의 거리는 최단거리이다.
다익스트라 알고리즘은 항상 간선의 거리 정보가 0 이상일 때만 사용할 수 있는데, 그 이유도 위 내용을 생각해보면 알 수 있다. dis[a] > dis[b] + d[b][a]가 성립하는 b가 존재하지 않아야하는데 d[b][a]가 음수가 될 수 있다면 저 조건이 성립하는 b점이 있을 수 있기 때문이다.
3. 구현
크게 두 가지 방식으로 구현할 수 있다. 시간복잡도가 O(V^2)인 방법과 O(ElogV)인 방법이다. 이때, V는 정점의 수, E는 간선의 수이다.
O(V^2)가 나오는 방식은 가장 가까운 정점을 찾는데 O(V)가 걸리고 이 행위를 V개의 정점에 대해 시행해주므로 O(V^2)가 걸린다.
여기서 가장 가까운 정점을 찾는데 굳이 O(V)로 돌지 않고 우선순위 큐를 이용하면 그 과정을 O(logV)에 시행할 수 있다.
우선순위 큐를 이용하여 구현해보겠다.
다익스트라 알고리즘 구현을 연습할 수 있는 문제가 있어 이 문제을 이용해 구현해보도록 하겠다.
https://www.acmicpc.net/problem/1753
import java.io.*;
import java.util.*;
public class Main {
static class Node implements Comparable<Node> {
int vertex;
int distance;
public Node(int vertex, int distance) {
this.vertex = vertex;
this.distance = distance;
}
@Override
public int compareTo(Node node) {
return this.distance <= node.distance ? -1 : 1;
}
}
static int v, e, start;
static int[] dis;
static ArrayList<ArrayList<Node>> arr = new ArrayList<ArrayList<Node>>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
v = Integer.parseInt(st.nextToken());
e = Integer.parseInt(st.nextToken());
start = Integer.parseInt(br.readLine());
dis = new int[v + 1];
for (int i = 0; i < v + 1; i++) {
arr.add(new ArrayList<>());
}
for (int i = 0; i < e; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int distance = Integer.parseInt(st.nextToken());
arr.get(from).add(new Node(to, distance)); // arr에 들어가는 Node 원소는 다음 정점과 간선 정보를 담는다.
}
Arrays.fill(dis, Integer.MAX_VALUE);
solve(start);
for (int i = 1; i < v + 1; i++) {
if (dis[i] == Integer.MAX_VALUE) {
sb.append("INF" + "\n");
} else {
sb.append(dis[i] + "\n");
}
}
bw.write(sb.toString());
br.close();
bw.flush();
bw.close();
}
static void solve(int x) {
PriorityQueue<Node> pq = new PriorityQueue<>();
dis[x] = 0;
pq.add(new Node(x, dis[x])); // pq에 들어가는 Node 원소는 정점과 시작점부터 그 정점까지의 최단 거리를 담는다.
while (!pq.isEmpty()) {
Node cur = pq.poll();
int curVertex = cur.vertex;
int xToCurDistance = cur.distance;
if (xToCurDistance > dis[curVertex]) {
continue;
}
for (Node child : arr.get(curVertex)) {
int nxtVertex = child.vertex;
int curToNxtDistance = child.distance;
if (xToCurDistance + curToNxtDistance < dis[nxtVertex]) {
dis[nxtVertex] = xToCurDistance + curToNxtDistance;
pq.add(new Node(nxtVertex, dis[nxtVertex]));
}
}
}
}
}'이론 > 알고리즘' 카테고리의 다른 글
| 이분 탐색 알고리즘 헷갈리는 내용 정리(while 조건, lo/hi 갱신 처리, 반환 값, lo/hi 범위) (1) | 2021.09.16 |
|---|---|
| 시간 복잡도 / 공간 복잡도 (0) | 2021.08.12 |
| 위상 정렬(Topological sorting) [Java] (0) | 2021.08.07 |
| 투 포인터 (0) | 2021.07.24 |
| 그리디 알고리즘 (0) | 2021.07.18 |