목차
1. 위상정렬이란?
2. 위상정렬의 과정
3. 위상정렬 구현
1. 위상정렬이란?
위상정렬은 사이클이 존재하지 않는 방향 그래프에서 정점들을 정렬하는 알고리즘이다. 대표적인 실생활의 예로 대학교의 선후수 교과과정이 있다.
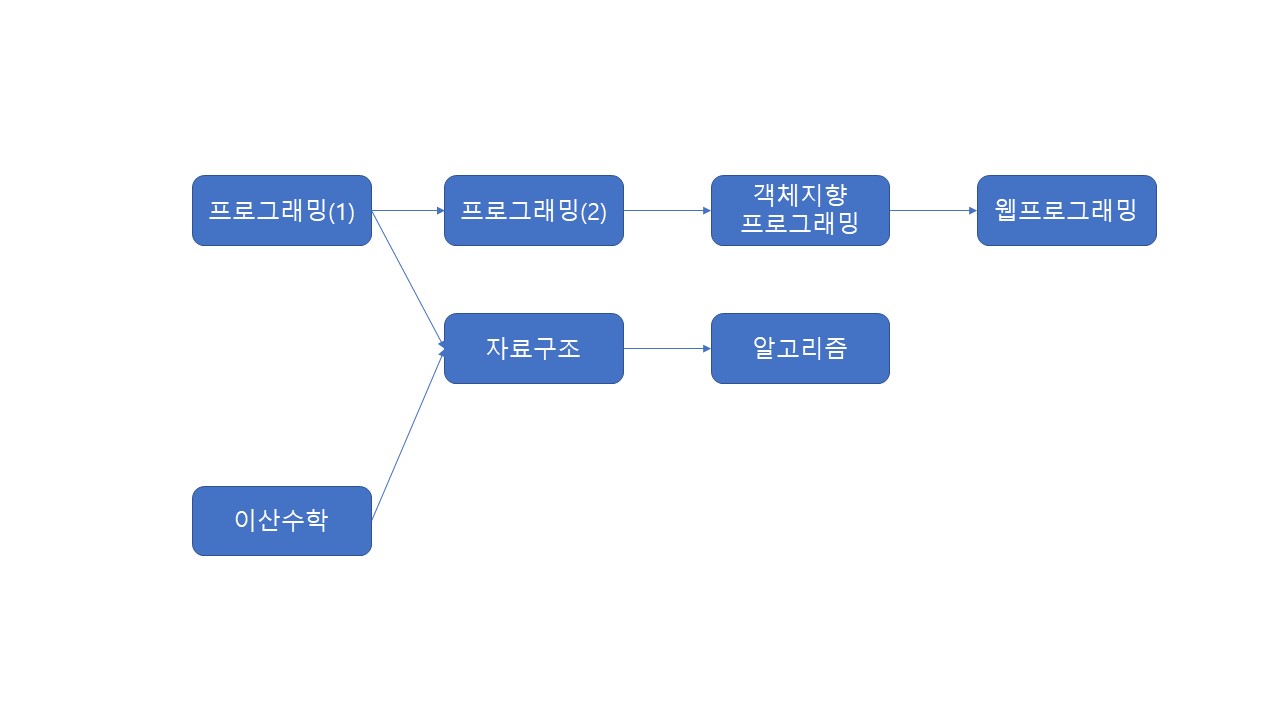
위와 같은 상황에서 과목을 듣는 순서를 짜는 것이 위상정렬의 한 예이다.
만약 사이클이 있다면 선후 관계가 모호해지기 때문에 사이클은 올 수 없다.
2. 위상정렬의 과정
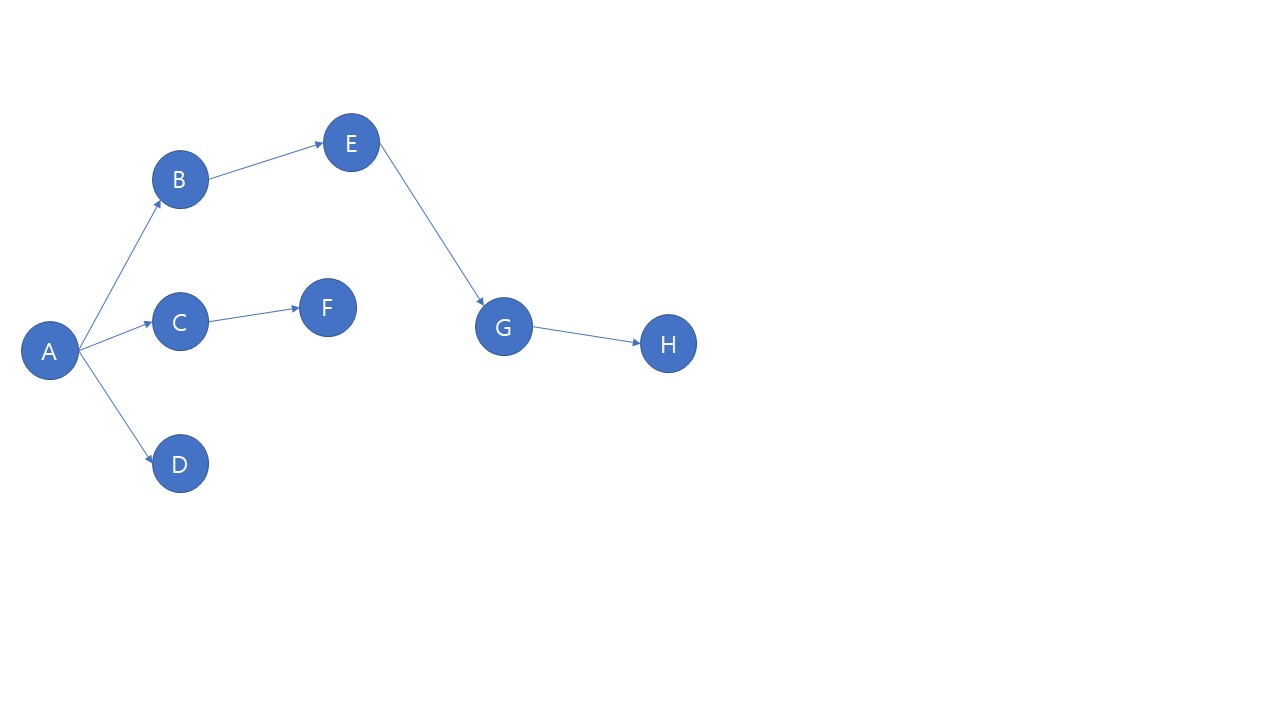
위 그래프를 한번 위상정렬해보자. 먼저 들어오는 간선이 없는 A가 제일 앞에 올 것이다. A에서 나가는 간선을 보면 B, C, D를 향해 있다. 이것의 의미는 B, C, D를 거치기 전에 반드시 A가 등장해야한다는 의미이다. 지금 상태에서는 A가 제일 앞에 등장했으니 A에서 나가는 간선은 의미가 없다. 그러므로 A와 A에서 나가는 간선들을 모두 지워준다.
들어오는 간선이 없는 정점으로 B, C, D가 있다. 모두 다 다음 순서로 올 수 있지만 편의상 여러 정점이 다음 순서로 올 수 있을 때 알파벳 순으로넣어주기로 한다. 다음 과정부터는 그림으로 살펴보자.
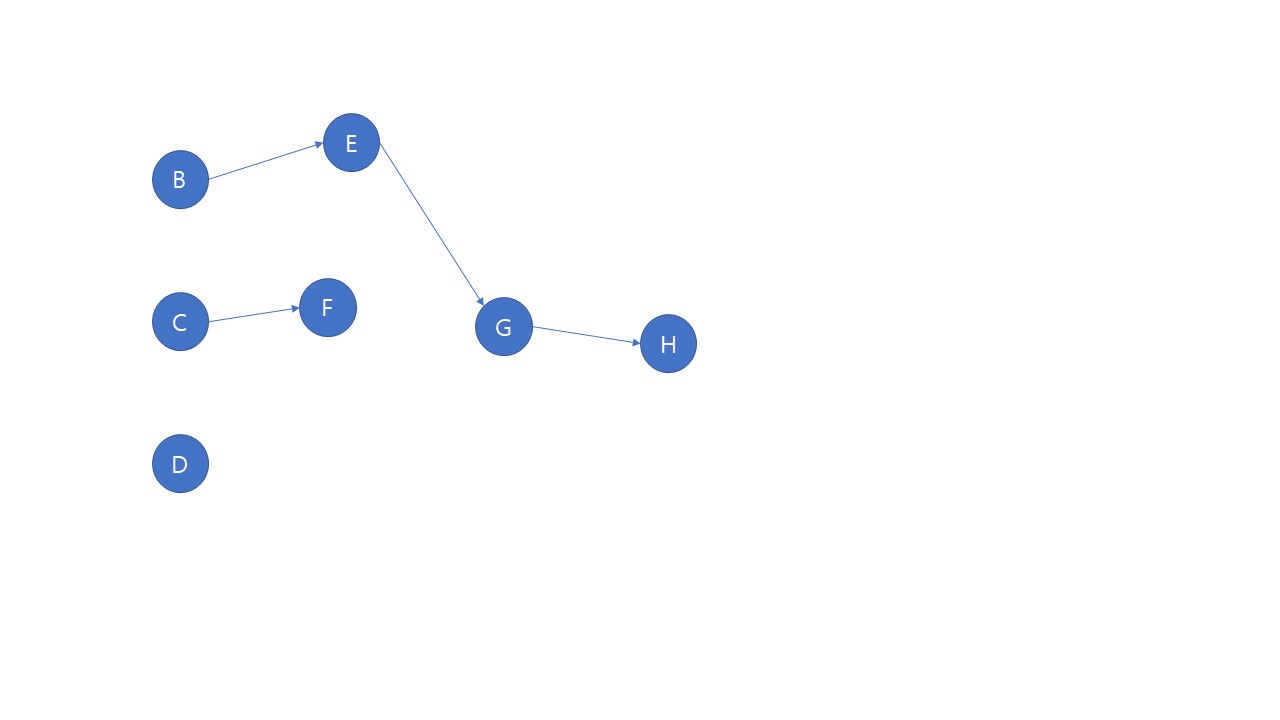
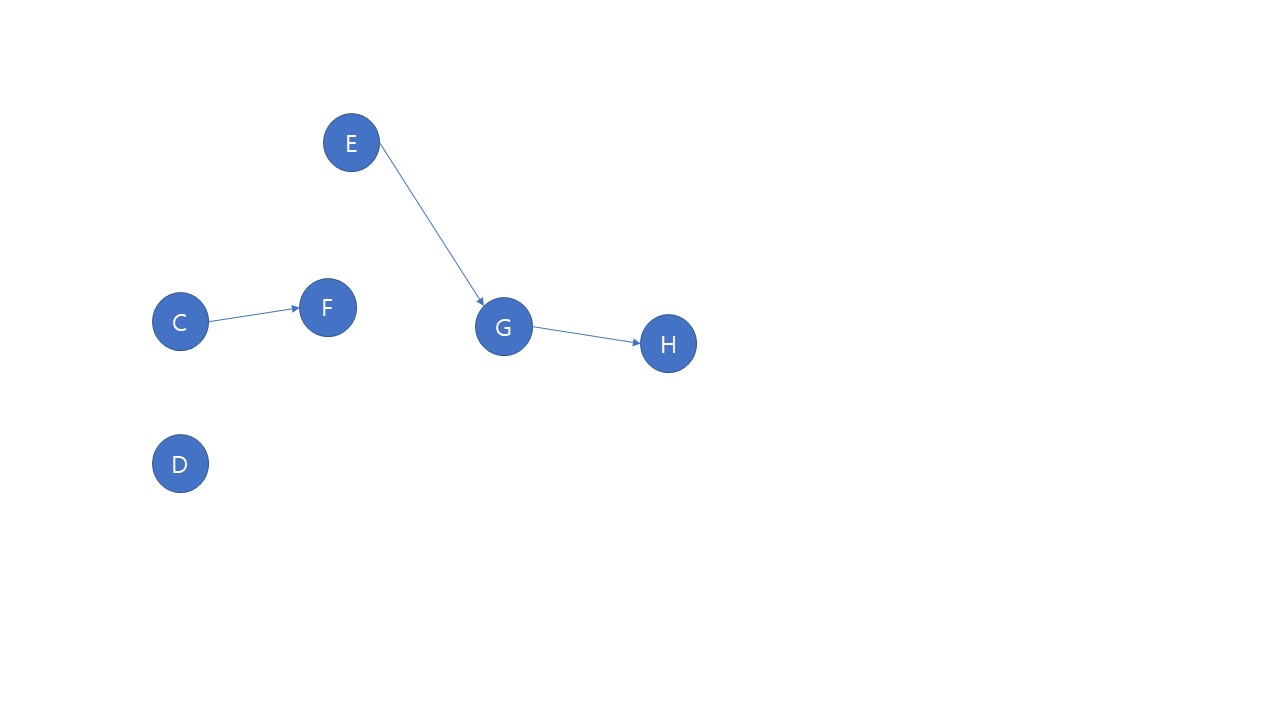
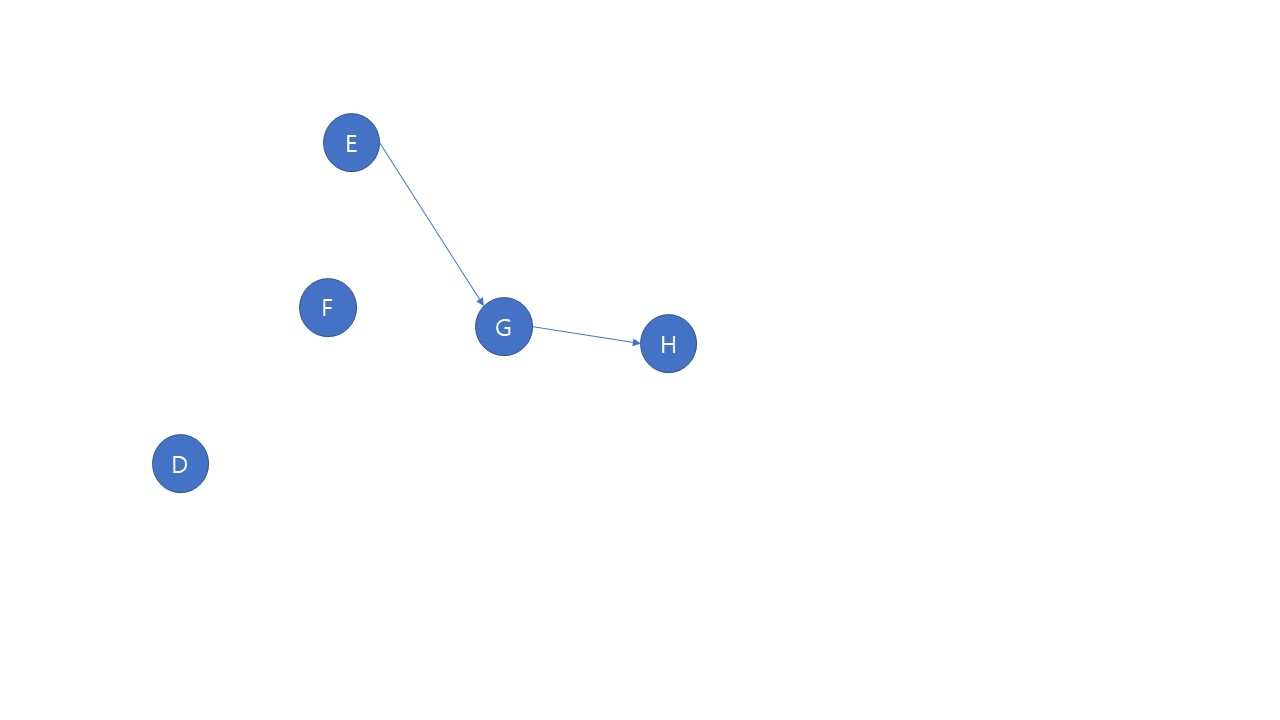
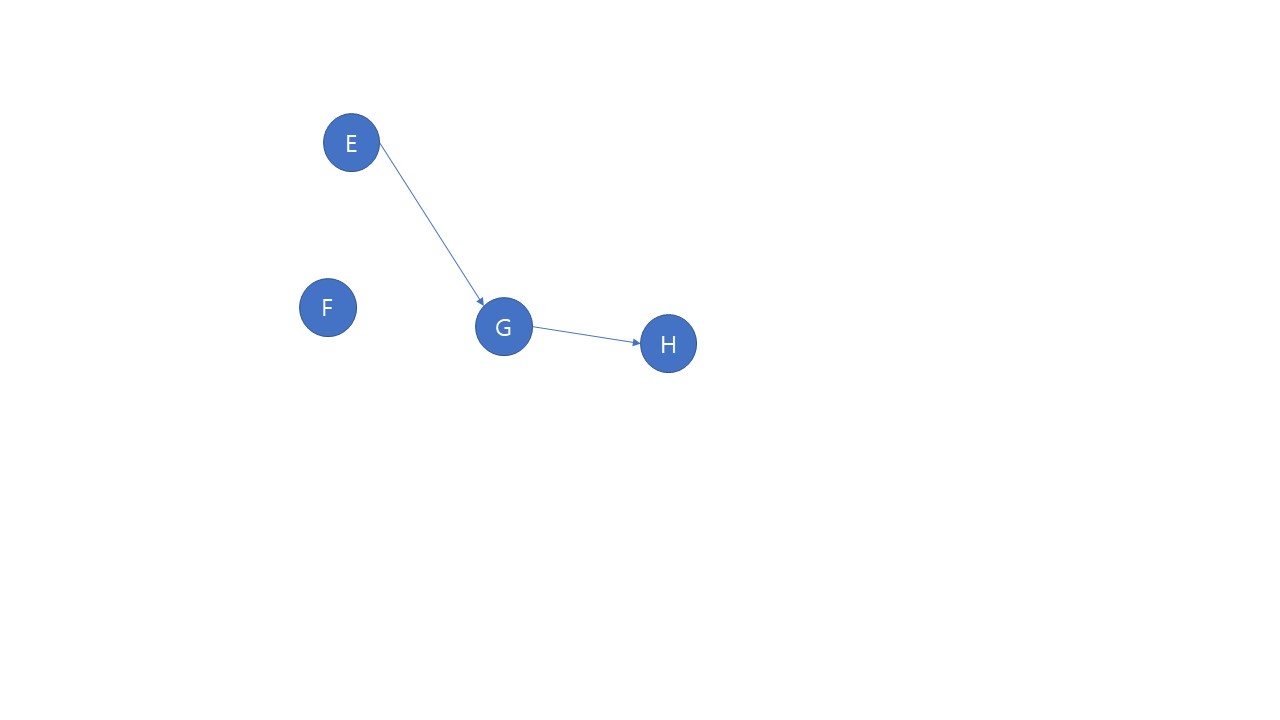
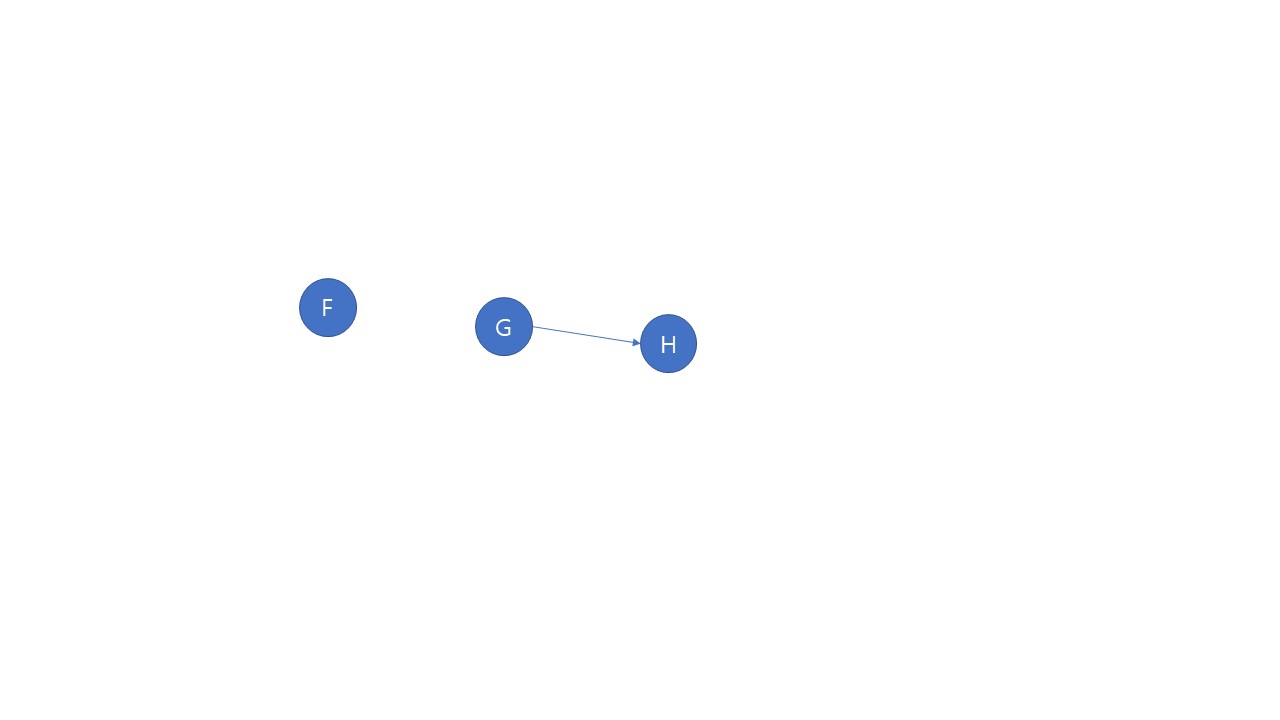
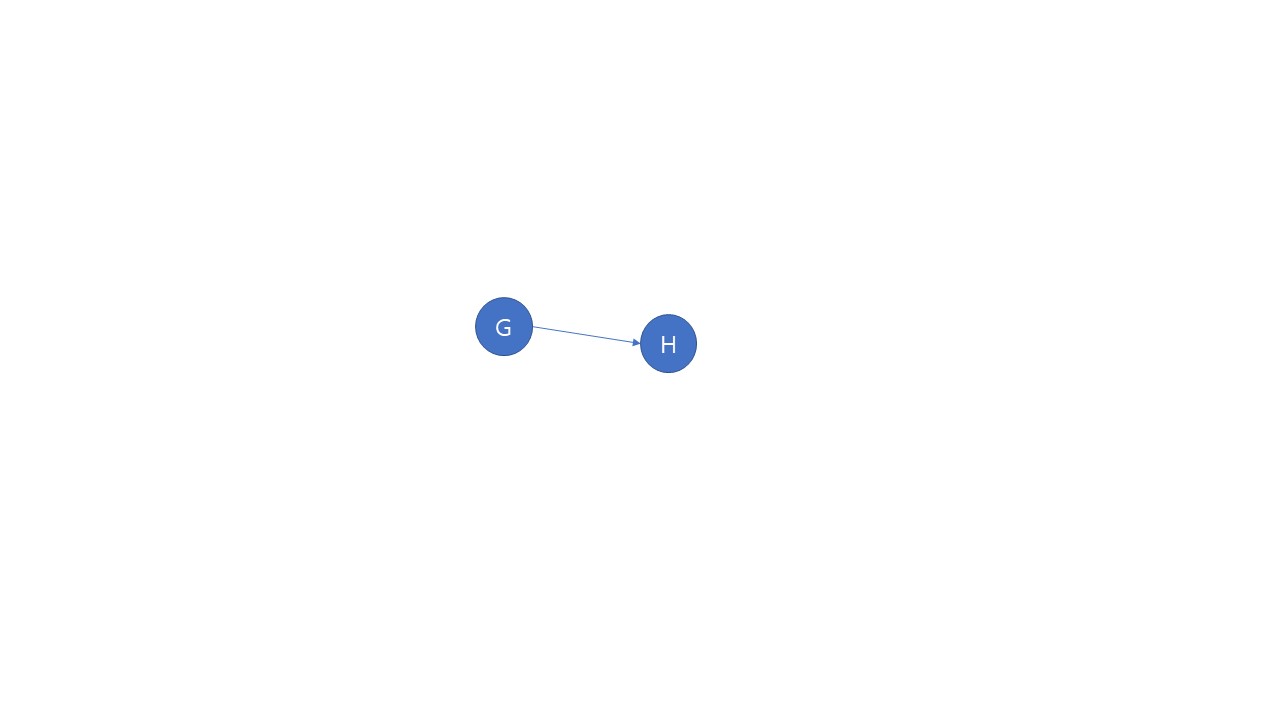

위상정렬의 결과는 A-B-C-D-E-F-G-H 이다.
3. 위상정렬 구현
1. 맨 처음 모든 정점에 들어오는 간선을 읽어 Indegree 테이블을 만들어준다.
2. Indegree가 0인 정점을 모두 큐에 넣는다.
3. 큐의 맨 앞에 있는 정점을 가져와 위상정렬 결과에 추가한다.
4. 해당 정점과 연결된 모든 정점의 indegree 값을 -1 해준다. 그리고 이 때, indegree 값이 0이 되면 큐에 넣어준다.
5. 큐가 빌 때까지 3, 4번 과정을 반복한다.
import java.util.*;
public class Main
{
static int n = 10;
static int[] indeg = new int[n + 1];
static List<List<Integer>> adj = new ArrayList<List<Integer>>();
static void Topo_sort()
{
Queue<Integer> q = new LinkedList<Integer>();
List<Integer> result = new ArrayList<Integer>();
for (int i = 1; i <= n; i++)
{
if (indeg[i] == 0)
q.offer(i);
}
while (!q.isEmpty())
{
int cur = q.poll();
result.add(cur);
for (int i = 0; i < adj.get(cur).size(); i++)
{
int nxt = adj.get(cur).get(i);
indeg[nxt]--;
if (indeg[nxt] == 0)
q.offer(nxt);
}
}
if (result.size() != n)
{
System.out.println("Cycle exists!");
return;
}
for (int i = 0; i < n; i++)
System.out.println(result.get(i) + " ");
}
}사이클에 포함된 정점은 indegree가 0이 될 수 없기에 큐에 들어갈 수 없다. 그러므로 그래프에 사이클이 있다면 위상정렬 결과에 모든 정점이 있지 않다는 말이다. 그렇기에 위상정렬을 돌려보는 것으로 그래프에 사이클이 있는지 알 수 있다.
위 방식의 위상정렬 알고리즘의 시간복잡도를 생각해보자. 각 정점은 큐에 1번씩 들어가고, 큐에 들어간 정점에 연결된 간선이 1번씩 -1되므로 시간복잡도는 O(V+E)이다.
'이론 > 알고리즘' 카테고리의 다른 글
| 이분 탐색 알고리즘 헷갈리는 내용 정리(while 조건, lo/hi 갱신 처리, 반환 값, lo/hi 범위) (1) | 2021.09.16 |
|---|---|
| 시간 복잡도 / 공간 복잡도 (0) | 2021.08.12 |
| 투 포인터 (0) | 2021.07.24 |
| 그리디 알고리즘 (0) | 2021.07.18 |
| 이분탐색(Binary search) (0) | 2021.07.11 |
![위상 정렬(Topological sorting) [Java]](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fu9yc4%2FbtrbuBvB6FN%2FAAAAAAAAAAAAAAAAAAAAALqZQLczopgcTOO2cBFuZrUXalT6jTa2SeMfp67YKSef%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DjDWYyhSbpLSUy4aJeZIoBALqfSU%253D)